Тело брошено со скоростью 20 м/с под углом 30° к горизонту... Решение задачи

Задача. Тело брошено со скоростью $v_{0}=20,0$ м/с под углом $\displaystyle \alpha =30^{\circ}$ к горизонту. Пренебрегая сопротивлением воздуха, найти скорость тела, а также его нормальное и тангенциальное ускорения через $t=1,50$ с после начала движения. На какое расстояние $l$ переместится за это время тело по горизонтали и на какой окажется высоте $h$?
Решение. Так как тело движется с постоянным ускорением $a=g$, его скорость и перемещение определяются векторными уравнениями

$\displaystyle v=v_{0}+at,\; \; \; \; \;$ (1.4),
$\displaystyle \Delta r=v_{0}t+\frac{at^{2}}{2},\; \; \; \; \;$ (1.5)
или соответствующими им скалярными уравнениями
$\displaystyle \left\{\begin{matrix} v_{x}=v_{0x}+a_{x}t,\\ \Delta x=v_{0x}t+\frac{a_{x}t^{2}}{2}; \end{matrix}\right.$ (1.19),
$\displaystyle \left\{\begin{matrix} v_{y}=v_{0y}+a_{y}t,\\ \Delta y=v_{0y}t+\frac{a_{y}t^{2}}{2}; \end{matrix}\right.$ (1.20).
Мы не знаем, в какой точке траектории будет тело через 1,50 с после начала движения, — на восходящей или нисходящей ветвях параболы. Предположим, что оно находится в точке $M$ (рис. 1).

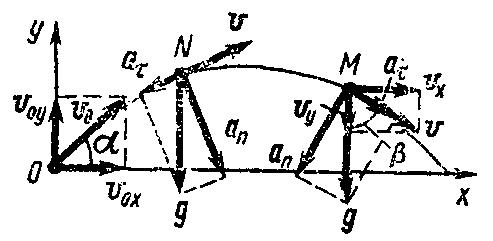
Рис. 1

Введем координатные оси, направленные по горизонтали $(Ox)$ и вертикали $(Oy)$ и совместим начало координат с положением тела в начальный момент времени. Тогда, подставив в уравнения (1.19), (1.20) значения $\displaystyle a_{x}=0,\: a_{y}=-g,\: v_{0x}=v_{0}\cos \alpha ;\; v_{0y}=v_{0}\sin \alpha,\: \Delta x=x,\: \Delta y=y$ и учитывая, что проекция скорости тела в точке $M$ на ось $Oy$ направлена вниз, получим:

$$\displaystyle v_{x}=v_{0}\cos \alpha ,\; \; \; \; \; \; \; (1)$$

$$\displaystyle x=v_{0}\cos \alpha \cdot t,\; \; \; \; \; \; \; (2)$$

$$\displaystyle -v_{y}=v_{0}\sin \alpha -gt,\; \; \; \; \; \; \; (3)$$

$$\displaystyle y=v_{0}\sin \alpha \cdot t-\frac{gt^{2}}{2}.\; \; \; \; \; \; \; \; (4)$$

Искомые величины $l,h$ равны соответственно координатам $x,y$ точки $M$ в момент $t=1,50$ с:

$\displaystyle l=x=v_{0}\cos \alpha \cdot t=20\cdot 0,87\cdot 1,5=26$ м.
$\displaystyle h=y=v_{0}\sin \alpha \cdot t-\frac{gt^{2}}{2}=20\cdot 0,5\cdot 1,5-\frac{9,8\cdot (1,5)^{2}}{2}=40$ м.
Скорость $v$ в точке $M$ найдем через ее проекции, определяемые по формулам (1) и (3):

$$\displaystyle v=\sqrt{v_{x}^{2}+v_{y}^{2}}=\sqrt{v_{0}^{2}\cos ^{2}\alpha +(gt-v_{0}\sin \alpha )^{2}}.\; \; (5)$$

Подставив числовые значения величин, получим

$\displaystyle v=\sqrt{20^{2}\cdot 0,87^{2}+(9,8\cdot 1,5-20\cdot 0,5)^{2}}=17$ м/с.

Для определения нормального и тангенциального ускорений учтем, что полное ускорение тела, движущегося в поле земного тяготения, есть не что иное как ускорение $g$ силы тяжести. Разложив вектор $g$ на составляющие по касательному и нормальному направлениям к траектории в точке $M$, получим (рис. 1):

$$\displaystyle a_{n}=g\sin \beta =g\frac{v_{x}}{v},$$

$$\displaystyle a_{\tau}=g\cos \beta =g\frac{v_{y}}{v},$$

где $\beta$ — угол между вертикалью и касательной к траектории в точке $M$. Подставим вместо величин $\displaystyle v_{x},v_{y},v$ их значения из формул (1), (3), (5):

$$\displaystyle a_{n}=\frac{gv_{0}\cos \alpha }{\sqrt{v_{0}^{2}\cos^{2} \alpha +(gt-v_{0}\sin \alpha )^{2}}},\; \; \; \; (6)$$

$$\displaystyle a_{\tau }=\frac{g(gt-v_{0}\sin \alpha)}{\sqrt{v_{0}^{2}\cos^{2} \alpha +(gt-v_{0}\sin \alpha )^{2}}}.\; \; \; \; (7)$$

Вычисления по формулам (6) и (7) дают:

$\displaystyle a_{n}=9,5$ м/с²; $\displaystyle a_{\tau}=2,6$ м/с².

Положительное значение величины $\displaystyle a_{\tau}$ подтверждает правильность нашего предположения относительно места тела на траектории. Отрицательное значение $\displaystyle a_{\tau}$ свидетельствовало бы, что скорость тела убывает и что, следовательно, оно находится на восходящей ветви параболы.

Замечания: 1. Предположим, что тело находится в данный момент в точке $N$ (рис. 1), тогда

$$\displaystyle v_{y}=v_{0}\sin \alpha -gt,\; \; \; \; \; \; \; (8)$$

$\displaystyle a_{\tau}=\frac{g(v_{0}\sin \alpha -gt)}{\sqrt{v_{0}^{2}\cos ^{2}\alpha +(v_{0}\sin \alpha -gt)^{2}}}=-2,6$ м/с².

Однако этот результат совпадает с полученным ранее. Дело в том, что в положении $N$ ускорение $\displaystyle a_{\tau}$ направлено против скорости $v$. Поэтому его отрицательное значение, вычисленное для $t=1,5$ с, свидетельствует о том, что фактически в этот момент ускорение $\displaystyle a_{\tau}$ имеет направление, противоположное тому, которое мы предположили, т. е. в сторону скорости $v$. Но это значит, что скорость растет, следовательно, тело движется по нисходящей ветви параболы. Таким образом, убеждаемся, что, приступая к решению задачи, можно произвольно задавать положение тела на траектории.

2. Величину $\displaystyle a_{\tau}$ можно найти другим путем, учитывая, что она, согласно формуле (1.7), равна производной от модуля скорости по времени. Подставив в (1.7) вместо скорости ее значение по (5) и выполнив дифференцирование, получим

$$\displaystyle a_{\tau }=\frac{dv}{dt}=\frac{g(gt-v_{0}\sin \alpha )}{\sqrt{v_{0}^{2}\cos ^{2}\alpha +(gt-v_{0}\sin \alpha )^{2}}}$$

независимо от того, будем ли подставлять значение $\displaystyle v_{y}$ по (3) или по (8). При таком методе нахождения $\displaystyle a_{\tau}$ неравенство