При движении автомобиля его колесо катится по окружности в горизонтальной плоскости... Решение задачи

Задача. При движении автомобиля его колесо радиуса $r=0,75$ м катится по окружности радиуса $R=6,00$ м в горизонтальной плоскости. При этом центр колеса движется с постоянной скоростью $v=1,50$ м/с. Определить: 1) угловую скорость и угловое ускорение колеса; 2) угол, образуемый вектором $\vec{\omega}$ с вертикалью.
Решение. Качение колеса по окружности представим как сумму двух вращательных движений:

1) с угловой скоростью $\vec{\omega_{1}}$ вокруг горизонтальной оси $AB$ (рис. 1) и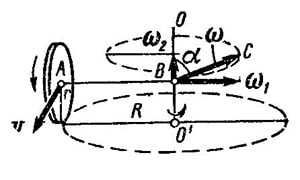

2) с угловой скоростью $\vec{\omega_{2}}$ вместе с осью $AB$ вокруг вертикальной оси $OO'$. Направление векторов $\vec{\omega_{1}},\vec{\omega_{2}}$ на рисунке соответствует правилу правого винта. Результирующий вектор угловой скорости по модулю равен

$$\displaystyle \vec{\omega}=\sqrt{\omega_{1}^{2}+\omega_{2}^{2}}\; \; \; \; \; \; \; \; \; (1)$$

Величины $\omega_{1},\omega_{2}$ найдем по второй из формул (*).

$$\displaystyle s=\varphi R,\: v=\omega R,\: a_{\tau}=\varepsilon R,\: a_{n}=\omega ^{2}R\; \; \; \; (*)$$

Предварительно определим линейную скорость наружных точек колеса в его вращении вокруг оси $AB$. Для этого все движения рассмотрим в системе отсчета, связанной с автомобилем. Тогда колесо будет вращаться вокруг неподвижной оси $AB$, а точки дороги, соприкасающиеся с колесом, будут в силу относительности движения иметь скорость $\displaystyle \vec{v'} =-\vec{v}$. Так как между колесом и дорогой нет скольжения, то его наружные точки также будут иметь скорость $\vec{v'}$, равную по модулю $\vec{v}$. Таким образом, из (1) и (*) получим

$$\displaystyle \omega=\sqrt{\left ( \frac{v}{r} \right )^{2}+\left ( \frac{v}{R} \right )^{2}}=\frac{v}{r}\sqrt{1+\frac{r^{2}}{R^{2}}}.$$

Как видно из чертежа, вектор $\vec{\omega}$ образует с вертикалью угол

$$\displaystyle \alpha =\textrm{arctg}\, \frac{\omega_{1}}{\omega_{2}}=\textrm{arctg}\frac{R}{r}=83^{\circ}.$$

Чтобы найти угловое ускорение колеса, учтем, что оно согласно определяющей его формуле (**),

$$\displaystyle \varepsilon =\frac{d\vec{\omega}}{dt}=\frac{d^{2}\vec{\varphi}}{dt^{2}}.\; \; \; \; (**)$$

равно скорости изменения вектора $\vec{\omega}$. Хотя при качении колеса модуль вектора $\vec{\omega}$ не изменяется, сам вектор изменяется: он поворачивается около оси $OO'$. Так как его начало (точка $B$ на рис. 1) неподвижно, то скорость изменения $\vec{\omega}$, т. е. величина $\varepsilon$, равна скорости перемещения конца вектора $\vec{\omega}$ — точки $C$. Точка $C$ опишет окружность радиуса, численно равного $\omega _{1}$, за время, равное периоду $T_{2}$ вращения колеса вокруг оси $OO'$, Поэтому с учетом (***)

$$\displaystyle \omega=2\pi n= \frac{2\pi}{T}\; \; \; \; \; \; (***)$$

получим

$\displaystyle \varepsilon =\frac{2\pi \omega _{1}}{T_{2}}=\omega _{2}\, \omega _{1}=\frac{v^{2}}{rR}=0,50$ рад/с².