В вагоне, движущемся горизонтально с постоянным ускорением, висит на проволоке груз... Решение задачи

Задача. В вагоне, движущемся горизонтально с постоянным ускорением $a=3,0$ м/с², висит на проволоке груз массой $m=2,00$ кг. Определить силу натяжения $\textbf{T}$ проволоки и угол $\alpha$ ее отклонения от вертикали, если груз неподвижен относительно вагона.

Решение. На груз действуют сила тяжести $m\textbf{g}$ и сила натяжения $\textbf{T}$ проволоки (рис. 1).

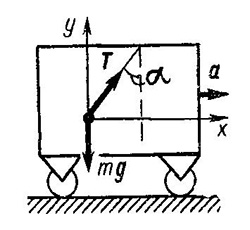
Так как груз неподвижен относительно вагона, его ускорение равно ускорению вагона. При этом нить должна быть отклоненной от вертикали назад, так как только в этом случае равнодействующая сил $m\textbf{g}$ и $\textbf{T}$ будет направлена вперед, сообщая грузу ускорение $\textbf{a}$. Второй закон Ньютона

$$\sum \textbf{F}=m\textbf{a},\; \; \; \; \; (*)$$

где $\sum \textbf{F}$ - равнодействующая всех сил, приложенных к телу,
в применении к грузу выразится уравнением

$$m \textbf{g}+\textbf{T}=m\textbf{a}.$$

Проектируя векторы $m \textbf{g},\textbf{T},m\textbf{a}$ на оси $x$ и $y$ (рис. 1), получим соответственно два скалярных уравнения:

$$T\sin \alpha =ma,\: T\cos \alpha -mg=0.$$

Совместное решение этих уравнений и последующее вычисление дают:

$$\displaystyle \alpha =\textrm{arctg}\frac{a}{g},\: T=m\sqrt{a^{2}+g^{2}};$$

$$\displaystyle \alpha =\textrm{arctg}\frac{3,0}{9,8}=\textrm{arctg}0,31=17^{\circ},\: T=2,0\sqrt{(3,0)^{2}+(9,8)^{2}}\, \textrm{H}.$$