Задача. Определить ускорения  и
и  , с которыми движутся грузы
, с которыми движутся грузы  и
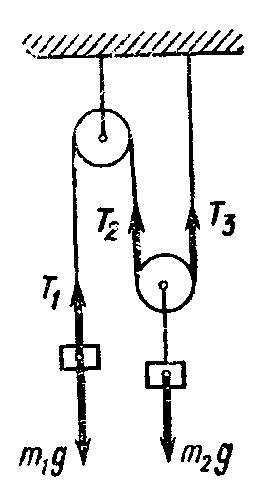
и  в установке, изображенной на рис. 1, а также силу натяжения
в установке, изображенной на рис. 1, а также силу натяжения  нити. Трением и массой блоков пренебречь. Нить считать невесомой и нерастяжимой.
нити. Трением и массой блоков пренебречь. Нить считать невесомой и нерастяжимой.
Решение. На груз  действуют силы тяжести
действуют силы тяжести  и сила натяжения
и сила натяжения  нити, на груз
нити, на груз  — сила тяжести
— сила тяжести  и силы натяжения
и силы натяжения  нитей. При этом
нитей. При этом  . Поскольку все силы направлены по вертикали, запишем уравнения, выражающие второй закон Ньютона, применительно к грузам сразу в скалярном виде, выбрав положительным направление вниз и предположив, что ускорение груза
. Поскольку все силы направлены по вертикали, запишем уравнения, выражающие второй закон Ньютона, применительно к грузам сразу в скалярном виде, выбрав положительным направление вниз и предположив, что ускорение груза  направлено вниз и, следовательно, ускорение груза
направлено вниз и, следовательно, ускорение груза  — вверх:
— вверх:


 . Очевидно, такое же соотношение существует и между модулями ускорений грузов:
. Очевидно, такое же соотношение существует и между модулями ускорений грузов:
Решив совместно уравнения (1), (2), (3), получим:

Отсюда следует: 1) если , то , т. е. ускорения грузов направлены так, как мы предположили; 2) если  , то
, то  — грузы покоятся или движутся равномерно; 3) если
— грузы покоятся или движутся равномерно; 3) если  , то
, то  . В этом случае ускорение груза
. В этом случае ускорение груза  направлено вверх, ускорение груза
направлено вверх, ускорение груза  — вниз. Замечание. Во всех трех случаях направления скоростей грузов остаются неопределенными, так как они зависят от направлений начальных скоростей и времени движения. Например, при груз
— вниз. Замечание. Во всех трех случаях направления скоростей грузов остаются неопределенными, так как они зависят от направлений начальных скоростей и времени движения. Например, при груз  может двигаться ускоренно вниз или замедленно вверх, В обоих случаях вектор
может двигаться ускоренно вниз или замедленно вверх, В обоих случаях вектор  направлен вниз,
направлен вниз,

