Тележку массой М, на которой лежит груз массой m, тянут с силой F. Найти ускорения тележки и груза. Решение задачи

Задача. Тележку массой $M$ = 20,0 кг, на которой лежит груз массой $m$ = 10,0 кг, тянут с силой $F$, направленной горизонтально (рис. 1). Коэффициент трения между грузом и тележкой $\mu =0,100$. Пренебрегая трением между тележкой и опорой, найти ускорения тележки $a_{1}$ и груза $a_{2}$, а также силу трения между грузом и тележкой в двух случаях: 1) $F$ = 2,00 кгс, 2) $F$ = 6,00 кгс.

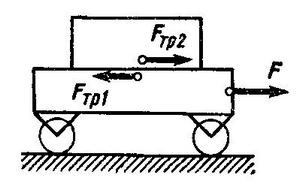
Решение. Рассмотрим силы, действующие на оба тела. При этом, поскольку их ускорения направлены по горизонтали, достаточно учитывать лишь силы, действующие горизонтально, так как остальные — направленные по вертикали — заведомо уравновешиваются.
На тележку действуют сила $\textbf{F}$ и сила со стороны груза $\textbf{F}_{TP1}$. Последняя направлена против скорости тележки относительно груза при трении скольжения или против силы $\textbf{F}$ при трении покоя, т. е. в любом случае сила $\textbf{F}_{TP}$ направлена влево (рис. 1). На груз действует сила трения со стороны тележки $\textbf{F}_{TP2}$, направленная, согласно третьему закону Ньютона, вправо, причем по модулю $F_{TP1}=F_{TP2}=F_{TP}$. Направив ось проекций в сторону ускорения, т. е. по горизонтали вправо, запишем в скалярном виде уравнения движения тележки и груза:

$$F-F_{TP}=Ma_{1},\; \; \; \; \; \; \; (1)$$

$$F_{TP}=ma_{2}.\; \; \; \; \; \; \; (2)$$

Уравнения (1), (2) содержат три неизвестных. Чтобы получить еще одно уравнение, выясним характер силы трения между тележкой и грузом. Если тележка выскальзывает из-под груза, то между ними действует сила трения скольжения, подчиняющаяся закону

$$F_{TP}=\mu N.$$

Так как в данном случае сила $N$ равна по модулю силе тяжести груза, то

$$F_{TP}=\mu mg.\; \; \; \; \; (3a)$$

Если же тележка и груз двигаются как одно целое, то между ними действует сила трения покоя $F_{\Pi OK}\neq \mu mg$. Однако в этом случае выполняется равенство

$$a_{1}=a_{2}.\; \; \; \; \; \; (3b)$$

Таким образом, в обоих возможных случаях получим систему трех уравнений.
Итак, необходимо выяснить характер сил трения, действующих между телами.
Рассмотрим подробнее оба возможных варианта:
а) тележка выскальзывает из-под груза. Между ними действует сила трения скольжения, которую найдем по формуле (За):

$$F_{TP}=0,100\cdot 10,0\cdot 9,8\, H=9,8\, H;$$

б) тележка и груз движутся как одно целое, удерживаемые трением покоя. Тогда, обозначив $a_{1}=a_{2}=a$, запишем систему уравнений (1), (2) в виде

$$F-F_{\Pi OK}=Ma,\; F_{\Pi OK}=ma.$$

Решив эту систему, получим

$$a=F/(M+m),\; \; \; \; \; \; (4)$$

$$F_{\Pi OK}=Fm/(M+m).\; \; \; \; \; \; (5)$$

Формула (5) выражает пропорциональную зависимость между $F$ и $F_{\Pi OK}$. Однако значение $F_{\Pi OK}$ имеет предел, равный силе $F_{TP}$, которая уже найдена. Поэтому в действительности два тела будут двигаться как одно целое лишь при таких значениях силы $F$, при которых значение $F_{\Pi OK}$, определяемое по (5), не будет превышать ее предельного значения. Проделав расчеты, получим:
1) если $F$ = 2,00 кгс = 19,6 Н, то $F_{\Pi OK}$ = 6,5 Н;
2) если $F$ = 6,00 кгс = 58,8 Н, то $F_{\Pi OK}$ = 19 Н,
что невозможно, ибо предельное значение $F_{\Pi OK}$ равно 9,8 Н. Значит, в этом случае между телами будет действовать трение скольжения.
Теперь легко ответить на все вопросы задачи:
1) $F$ = 19,6 Н. Между телами действует сила трения покоя $F_{\Pi OK}$ = 6,5 Н. Из формулы (4) находим $a$ = 0,65 м/с²;
2) $F$ = 58,8 Н. Между телами действует сила трения скольжения $F_{TP}$=9,8 Н. Из (1) и (2) находим ускорения тел: $a_{1}$ = 2,5 м/с², $a_{2}$ = 0,98м/с².