Из двух пунктов А и B, расстояние между которыми l, одновременно начинают двигаться два корабля со скоростями... Решение задачи

Задача. Из двух пунктов $A$ и $B$, расстояние между которыми $l$, одновременно начинают двигаться два корабля со скоростями $v_{1}$ и $v_{2}$. Векторы скоростей образуют с отрезком $AB$ одинаковые углы $\alpha =45^{\circ}$ (рис. 1). Считая движение кораблей равномерным и прямолинейным, определить наименьшее расстояние между ними.

Рис. 1

Решение. Приведем два способа решения задачи, отличающиеся выбором системы отсчета.
1. Пусть движение кораблей происходит в той системе отсчета (связанной с Землей), в которой заданы их скорости. Сначала расстояние между кораблями будет уменьшаться, затем (если они не столкнутся) — увеличиваться. Чтобы найти наименьшее расстояние $s_{min}$, применим общий метод исследования функции на экстремум. Для этого рассмотрим положение кораблей спустя произвольный промежуток времени $t$ после начала движения и найдем расстояние между ними как функцию времени. Из чертежа следует:

$$s=\sqrt{(OM)^{2}+(ON)^{2}}=\sqrt{(OA-v_{1}t)^{2}+(OB-v_{2}t)^{2}}.$$

Обозначив $a=OA=OB$, получим

$$\displaystyle s=\sqrt{2a^{2}-2a(v_{1}+v_{2})t+(v^{2}_{1}+v^{2}_{2})t^{2}}.\; \; \; \; \; \; (1)$$

Чтобы найти минимум функции $s=s(t)$, продифференцируем ее по времени и приравняем нулю производную:

$$\displaystyle \frac{ds}{dt}=\frac{-2a(v_{1}+v_{2})+2t(v^{2}_{1}+v^{2}_{2})}{2\sqrt{2a^{2}-2a(v_{1}+v_{2})t+(v^{2}_{1}+v^{2}_{2})t^{2}}}=0.$$

Отсюда время, соответствующее наименьшему расстоянию $s_{min}$, равно

$$\displaystyle t_{min}=\frac{a(v_{1}+v_{2})}{v^{2}_{1}+v^{2}_{2}}.$$

Подставив это значение времени в (1), получим ответ:

$$\displaystyle s_{min}=\frac{a\left |v_{2}-v_{1} \right |}{\sqrt{v^{2}_{1}+v^{2}_{2}}}=\frac{l\left |v_{2}-v_{1} \right |}{\sqrt{2(v^{2}_{1}+v^{2}_{2})}}.\; \; \; \; \; \; \; \; \; (2)$$

Из формулы (2) следует: 1) если $v_{1}=v_{2}$, то $s_{min}=0$, т. е., двигаясь с одинаковыми скоростями, корабли встретятся в точке $O$ (рис. 1); 2) если $v_{1}=0$ или $v_{2}=0$ (движется только один корабль), то $s_{min}=a$, т. е. $s=s_{min}$, когда корабль окажется в точке $O$.

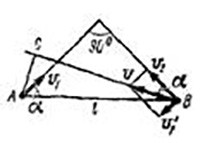
Рис. 2

2. Воспользуемся системой отсчета, связанной с одним из двух кораблей, например с первым. В этой системе отсчета первый корабль будет неподвижен, а движение второго корабля будет сложным: со скоростью $v_{2}$ относительно Земли и со скоростью $v'_{1}=-v_{1}$, вместе с Землей относительно первого корабля (рис. 2). Скорость результирующего движения выразится вектором $v$, причем

$$\displaystyle v=\sqrt{{v}'^{2}_{1}+v^{2}_{2}}=\sqrt{v^{2}_{1}+v^{2}_{2}}.$$

Минимальным расстоянием между кораблями будет длина перпендикуляра $AC$, опущенного на направление вектора $v$. Расчет, основанный на подобии прямоугольных треугольников, приводит к ответу

$$\displaystyle s_{min}=AC=\frac{l(v_{2}-v_{1})}{\sqrt{2(v^{2}_{1}+v^{2}_{2})}},\; \; \; \; \; \; \; \; (3)$$

что совпадает с ответом (2), так как в (3)