Частица A, двигаясь со скоростью v, ударяется о массивную стенку B... Решение задачи

Задача. Частица $A$ , двигаясь со скоростью $\vec{v}$ , ударяется о массивную стенку $B$ , которая движется в том же направлении со скоростью $\vec{u}$ (рис. 1). Определить скорость частицы после удара, если известно, что при ударе о стенку $B$ , когда она неподвижна, частица отскакивает, сохраняя скорость по модулю и изменяя ее направление на противоположное.

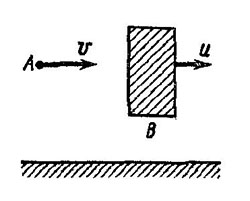
Рис. 1

Решение. Условие задачи предполагает скорости движения тел $A$ к $B$ заданными в некоторой системе отсчета, например, связанной с Землей. Но при этом дан закон соударения частицы с неподвижной стенкой. Поэтому, для того чтобы решить задачу, необходимо рассмотреть движение частицы в системе отсчета, связанной со стенкой $B$ . В этой системе отсчета стенка будет неподвижной, а движение частицы — сложным, состоящим из двух: относительно Земли со скоростью $\vec{v}$ и, как это следует из соотношения

$\vec{v_{2}}=-\vec{v_{1}},$

вместе с Землей относительно стенки со скоростью

$\vec{-u}$ . Поэтому в соответствии с формулой

$\vec{v}=\vec{v_{1}}+\vec{v_{2}},$

скорость частицы относительно стенки равна

$\vec{v}+(-\vec{u})=\vec{v}-\vec{u}.$

Согласно условию частица отскочит от стенки со скоростью

$-(\vec{v}-\vec{u})=\vec{u}-\vec{v}.$

Теперь вернемся к системе отсчета, связанной с Землей, так как в этой системе надо найти скорость частицы после удара. Движение частицы после удара о стенку и в этом случае состоит из двух: относительно стенки со скоростью